Process Capability Analysis in Excel with UNISTAT
The UNISTAT statistics add-in extends Excel with Process Capability Analysis capabilities.
For further information visit UNISTAT User's Guide section 9.3.6. Process Capability Analysis.
Here we provide a sample output from the UNISTAT Excel statistics add-in for data analysis.
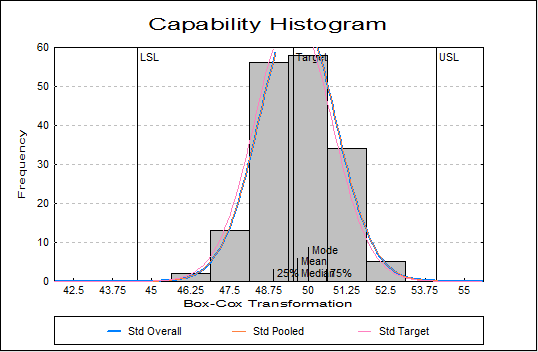
Process Capability Analysis
Process Data
Variables Selected: THICKNESS
Subsample selected by: ZONE = 1, 2, 3, 4
Number of Cases: 168
| Number of Subgroups | 4 |
|---|---|
| Control Range | 6.0000 |
| Original Process Data: | |
| LSL | 460.0000 |
| Target | 560.0000 |
| USL | 660.0000 |
| Mean | 563.0357 |
| Overall Standard Deviation | 25.3847 |
| Pooled Standard Deviation | 25.5069 |
| Transformed Process Data: | |
| LSL | 44.5338 |
| Target | 49.5291 |
| USL | 54.1107 |
| Mean | 49.6607 |
| Overall Standard Deviation | 1.2080 |
| Pooled Standard Deviation | 1.2137 |
Data Transformation: Results
| Lambda | 0.5192 |
|---|
Box-Cox Transformation:
y = (y ^ Lambda – 1) / Lambda
y = (POWER(y, 0.519150639529349) – 1) / 0.519150639529349
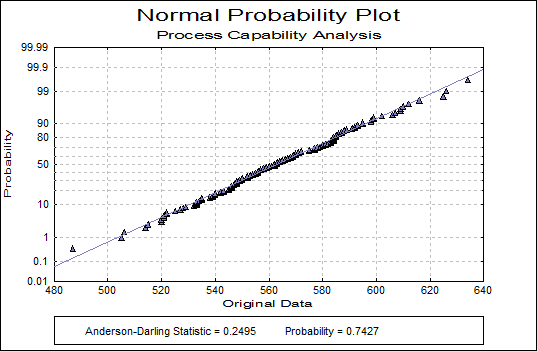
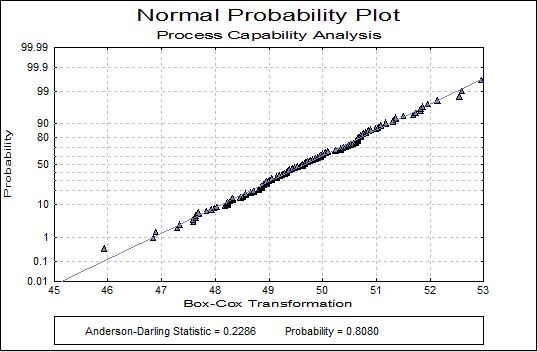
Normality Tests
Smaller probabilities indicate non-normality.
| Anderson-Darling Statistic | Probability | |
|---|---|---|
| Original Data | 0.2495 | 0.7427 |
| Transformed Data | 0.2286 | 0.8080 |
Transformed Data
| Original Data | Transformed Data | Group | |
|---|---|---|---|
| 1 | 487.0000 | 45.9301 | 3 |
| 2 | 505.0000 | 46.8403 | 3 |
| 3 | 506.0000 | 46.8904 | 4 |
| 4 | 514.0000 | 47.2896 | 4 |
| 5 | 515.0000 | 47.3393 | 1 |
| 6 | 520.0000 | 47.5870 | 1 |
| 7 | 520.0000 | 47.5870 | 3 |
| 8 | 521.0000 | 47.6364 | 3 |
| 9 | 521.0000 | 47.6364 | 4 |
| 10 | 522.0000 | 47.6858 | 1 |
| 11 | 522.0000 | 47.6858 | 3 |
| 12 | 525.0000 | 47.8336 | 2 |
| 13 | 527.0000 | 47.9319 | 3 |
| 14 | 528.0000 | 47.9810 | 1 |
| 15 | 529.0000 | 48.0301 | 4 |
| 16 | 532.0000 | 48.1770 | 4 |
| 17 | 533.0000 | 48.2258 | 4 |
| 18 | 533.0000 | 48.2258 | 3 |
| 19 | 533.0000 | 48.2258 | 2 |
| 20 | 533.0000 | 48.2258 | 4 |
| 21 | 534.0000 | 48.2747 | 4 |
| 22 | 535.0000 | 48.3234 | 2 |
| 23 | 535.0000 | 48.3234 | 2 |
| 24 | 535.0000 | 48.3234 | 1 |
| 25 | 538.0000 | 48.4695 | 2 |
| 26 | 539.0000 | 48.5181 | 1 |
| 27 | 539.0000 | 48.5181 | 4 |
| 28 | 540.0000 | 48.5667 | 1 |
| 29 | 540.0000 | 48.5667 | 4 |
| 30 | 540.0000 | 48.5667 | 3 |
| 31 | 542.0000 | 48.6637 | 4 |
| 32 | 542.0000 | 48.6637 | 2 |
| 33 | 543.0000 | 48.7121 | 3 |
| 34 | 543.0000 | 48.7121 | 4 |
| 35 | 545.0000 | 48.8089 | 2 |
| 36 | 545.0000 | 48.8089 | 4 |
| 37 | 545.0000 | 48.8089 | 1 |
| 38 | 546.0000 | 48.8572 | 3 |
| 39 | 546.0000 | 48.8572 | 1 |
| 40 | 546.0000 | 48.8572 | 4 |
| 41 | 546.0000 | 48.8572 | 3 |
| 42 | 546.0000 | 48.8572 | 1 |
| 43 | 547.0000 | 48.9055 | 1 |
| 44 | 547.0000 | 48.9055 | 3 |
| 45 | 547.0000 | 48.9055 | 4 |
| 46 | 548.0000 | 48.9537 | 2 |
| 47 | 548.0000 | 48.9537 | 2 |
| 48 | 548.0000 | 48.9537 | 1 |
| 49 | 548.0000 | 48.9537 | 2 |
| 50 | 548.0000 | 48.9537 | 3 |
| 51 | 549.0000 | 49.0019 | 4 |
| 52 | 549.0000 | 49.0019 | 1 |
| 53 | 550.0000 | 49.0500 | 1 |
| 54 | 550.0000 | 49.0500 | 1 |
| 55 | 550.0000 | 49.0500 | 1 |
| 56 | 550.0000 | 49.0500 | 4 |
| 57 | 552.0000 | 49.1461 | 4 |
| 58 | 552.0000 | 49.1461 | 3 |
| 59 | 552.0000 | 49.1461 | 1 |
| 60 | 553.0000 | 49.1942 | 3 |
| 61 | 553.0000 | 49.1942 | 2 |
| 62 | 554.0000 | 49.2421 | 3 |
| 63 | 554.0000 | 49.2421 | 1 |
| 64 | 555.0000 | 49.2901 | 1 |
| 65 | 555.0000 | 49.2901 | 2 |
| 66 | 555.0000 | 49.2901 | 1 |
| 67 | 556.0000 | 49.3379 | 4 |
| 68 | 556.0000 | 49.3379 | 3 |
| 69 | 556.0000 | 49.3379 | 3 |
| 70 | 556.0000 | 49.3379 | 1 |
| 71 | 556.0000 | 49.3379 | 2 |
| 72 | 557.0000 | 49.3858 | 1 |
| 73 | 557.0000 | 49.3858 | 1 |
| 74 | 558.0000 | 49.4336 | 4 |
| 75 | 558.0000 | 49.4336 | 2 |
| 76 | 558.0000 | 49.4336 | 4 |
| 77 | 558.0000 | 49.4336 | 2 |
| 78 | 559.0000 | 49.4814 | 2 |
| 79 | 560.0000 | 49.5291 | 3 |
| 80 | 560.0000 | 49.5291 | 3 |
| 81 | 561.0000 | 49.5768 | 1 |
| 82 | 562.0000 | 49.6244 | 3 |
| 83 | 562.0000 | 49.6244 | 1 |
| 84 | 562.0000 | 49.6244 | 2 |
| 85 | 563.0000 | 49.6720 | 4 |
| 86 | 563.0000 | 49.6720 | 3 |
| 87 | 563.0000 | 49.6720 | 2 |
| 88 | 563.0000 | 49.6720 | 2 |
| 89 | 563.0000 | 49.6720 | 4 |
| 90 | 564.0000 | 49.7196 | 3 |
| 91 | 564.0000 | 49.7196 | 2 |
| 92 | 564.0000 | 49.7196 | 1 |
| 93 | 565.0000 | 49.7671 | 1 |
| 94 | 566.0000 | 49.8146 | 4 |
| 95 | 566.0000 | 49.8146 | 2 |
| 96 | 567.0000 | 49.8620 | 3 |
| 97 | 567.0000 | 49.8620 | 3 |
| 98 | 567.0000 | 49.8620 | 2 |
| 99 | 568.0000 | 49.9094 | 1 |
| 100 | 568.0000 | 49.9094 | 1 |
| 101 | 569.0000 | 49.9568 | 2 |
| 102 | 569.0000 | 49.9568 | 4 |
| 103 | 569.0000 | 49.9568 | 4 |
| 104 | 569.0000 | 49.9568 | 1 |
| 105 | 570.0000 | 50.0041 | 4 |
| 106 | 570.0000 | 50.0041 | 2 |
| 107 | 570.0000 | 50.0041 | 1 |
| 108 | 571.0000 | 50.0514 | 4 |
| 109 | 571.0000 | 50.0514 | 3 |
| 110 | 572.0000 | 50.0986 | 3 |
| 111 | 572.0000 | 50.0986 | 3 |
| 112 | 572.0000 | 50.0986 | 2 |
| 113 | 575.0000 | 50.2401 | 4 |
| 114 | 575.0000 | 50.2401 | 4 |
| 115 | 577.0000 | 50.3342 | 2 |
| 116 | 577.0000 | 50.3342 | 3 |
| 117 | 577.0000 | 50.3342 | 3 |
| 118 | 577.0000 | 50.3342 | 3 |
| 119 | 578.0000 | 50.3812 | 2 |
| 120 | 579.0000 | 50.4281 | 3 |
| 121 | 580.0000 | 50.4751 | 4 |
| 122 | 580.0000 | 50.4751 | 2 |
| 123 | 580.0000 | 50.4751 | 1 |
| 124 | 581.0000 | 50.5220 | 1 |
| 125 | 581.0000 | 50.5220 | 2 |
| 126 | 582.0000 | 50.5688 | 3 |
| 127 | 583.0000 | 50.6156 | 1 |
| 128 | 583.0000 | 50.6156 | 2 |
| 129 | 583.0000 | 50.6156 | 3 |
| 130 | 584.0000 | 50.6624 | 1 |
| 131 | 584.0000 | 50.6624 | 2 |
| 132 | 584.0000 | 50.6624 | 4 |
| 133 | 584.0000 | 50.6624 | 2 |
| 134 | 584.0000 | 50.6624 | 4 |
| 135 | 584.0000 | 50.6624 | 1 |
| 136 | 584.0000 | 50.6624 | 2 |
| 137 | 585.0000 | 50.7091 | 4 |
| 138 | 585.0000 | 50.7091 | 2 |
| 139 | 585.0000 | 50.7091 | 2 |
| 140 | 586.0000 | 50.7558 | 4 |
| 141 | 586.0000 | 50.7558 | 4 |
| 142 | 587.0000 | 50.8025 | 2 |
| 143 | 587.0000 | 50.8025 | 2 |
| 144 | 588.0000 | 50.8491 | 2 |
| 145 | 588.0000 | 50.8491 | 2 |
| 146 | 589.0000 | 50.8956 | 3 |
| 147 | 591.0000 | 50.9887 | 4 |
| 148 | 592.0000 | 51.0351 | 4 |
| 149 | 592.0000 | 51.0351 | 1 |
| 150 | 593.0000 | 51.0816 | 2 |
| 151 | 593.0000 | 51.0816 | 1 |
| 152 | 595.0000 | 51.1743 | 1 |
| 153 | 595.0000 | 51.1743 | 4 |
| 154 | 598.0000 | 51.3131 | 3 |
| 155 | 598.0000 | 51.3131 | 3 |
| 156 | 599.0000 | 51.3593 | 4 |
| 157 | 599.0000 | 51.3593 | 2 |
| 158 | 602.0000 | 51.4977 | 2 |
| 159 | 606.0000 | 51.6817 | 4 |
| 160 | 607.0000 | 51.7276 | 4 |
| 161 | 609.0000 | 51.8193 | 3 |
| 162 | 609.0000 | 51.8193 | 1 |
| 163 | 610.0000 | 51.8651 | 1 |
| 164 | 612.0000 | 51.9566 | 3 |
| 165 | 616.0000 | 52.1392 | 3 |
| 166 | 625.0000 | 52.5478 | 3 |
| 167 | 626.0000 | 52.5930 | 1 |
| 168 | 634.0000 | 52.9536 | 3 |
Performance: Parts Per Million
| PPM < LSL | PPM > USL | PPM Total | |
|---|---|---|---|
| Observed | 0.0000 | 0.0000 | 0.0000 |
| Overall | 10.9778 | 114.9291 | 125.9069 |
| Pooled | 11.9928 | 122.9638 | 134.9566 |
Performance: Percent
| % < LSL | % > USL | % Total | |
|---|---|---|---|
| Observed | 0.0000 | 0.0000 | 0.0000 |
| Overall | 0.0011 | 0.0115 | 0.0126 |
| Pooled | 0.0012 | 0.0123 | 0.0135 |
Capability Indices: Overall Standard Deviation
| Value | Lower 95% | Upper 95% | |
|---|---|---|---|
| Cp | 1.3213 | 1.1796 | 1.4628 |
| Cpl | 1.4147 | 1.2548 | 1.5745 |
| Cpu | 1.2279 | 1.0869 | 1.3689 |
| Bissell Cpk | 1.2279 | 1.0869 | 1.3689 |
| ZSW Eq 6 Cpk | 1.2279 | 1.0947 | 1.3611 |
| ZSW Eq 8 Cpk | 1.2279 | 1.0854 | 1.3704 |
| Chan Cpm | 1.2567 | 1.1433 | 1.3686 |
| Boyles Cpm | 1.2605 | 1.1467 | 1.3727 |
| Modified Boyles Cpm | 1.3135 | 1.1766 | 1.4580 |
| NIST Cpm | 1.3135 | 1.1731 | 1.4537 |
| Cpmk | 1.2243 | 1.1461 | 1.3024 |
| Cs | 1.4041 | ||
| Cpm+ | 0.0066 | ||
| Cjkp | 1.1609 |
Capability Indices: Pooled Standard Deviation
| Value | Lower 95% | Upper 95% | |
|---|---|---|---|
| Cp | 1.3151 | 1.1728 | 1.4572 |
| Cpl | 1.4080 | 1.2475 | 1.5685 |
| Cpu | 1.2222 | 1.0806 | 1.3637 |
| Bissell Cpk | 1.2222 | 1.0806 | 1.3637 |
| Ccpk | 1.2583 |
Capability Indices: Nonparametric
Quantile Method: Simple Average
Interval Method: Normal Approximation
| Value | Lower 95% | Upper 95% | |
|---|---|---|---|
| Median | 49.6482 | 49.3379 | 49.8620 |
| 0.5% Quantile | 45.9301 | * | 47.2896 |
| 99.5% Quantile | 52.9536 | 52.1392 | * |
| Cnpk | 1.3501 |