6.3.4. Outlier Tests

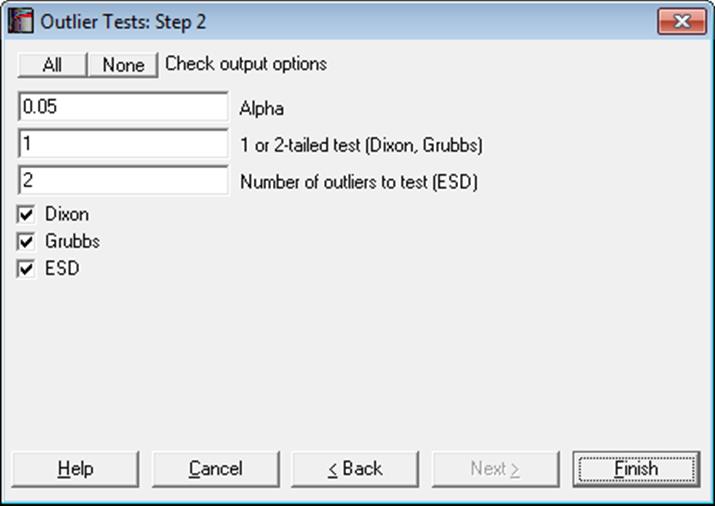
The three outlier tests supported here will detect whether a minimum or a maximum value is an outlier and test its significance by comparing the test statistic with a critical value. The critical table values are generated by the program for any alpha level, not just for 1%, 5%, 10%. For Dixon and Grubbs tests, if the one-tail option is selected, a separate one-tailed test is performed for the minimum and maximum values of data. If a two-tailed test is selected the larger of the minimum and maximum test values is tested against a two-tailed table value. ESD test is two-tailed only.

If significant outlier(s) are found, their values are displayed in a separate table.

6.3.4.1. Dixon

Dixon’s test does not assume normal distribution of data and is useful in detecting outliers in small sized groups.

The data is sorted in ascending order and two separate Q values are obtained for the lowest and highest values in data. Separate tests are performed for minimum and maximum values according to formulas given by Dixon (1953).

	Minimum	Maximum
3 ≤ n ≤ 7
8 ≤ n ≤ 10
11 ≤ n ≤ 13
14 ≤ n ≤ 1000

 

If a two-tailed test is selected, the larger of the Q_Min and Q_Max is tested against the table value computed for alpha / 2. Note that the one-tail table Q is very accurate but the two-tailed Q is an approximation.

Example

Sachs, L. (1984), p. 278 gives the following four observations 157, 326, 177, 176 and finds that 326 is an outlier at 5% level (one-tailed test).

Dixon’s Outlier Test

Alpha = 0.05

One-tailed tests

	Dixon’s Q	Table Q	Pass/Fail
C1 Q(Min)	0.1124	0.7655	Pass
Q(Max)	0.8817	0.7655	**Fail**

N = 4, Q(Min)=(X(2)-X(1))/(X(N)-X(1)), Q(Max)=(X(N)-X(N-1))/(X(N)-X(1))

 

	Outlier Value
C1	326

 

On the other hand, although in the sequence 1, 2, 3, 4, 5, 9 the value 9 looks like an outlier, it is not significantly different from the rest of the numbers at 5% level.

Dixon’s Outlier Test

Alpha = 0.05

One-tailed tests

	Dixon’s Q	Table Q	Pass/Fail
C1 Q(Min)	0.1250	0.5624	Pass
Q(Max)	0.5000	0.5624	Pass

N = 6, Q(Min)=(X(2)-X(1))/(X(N)-X(1)), Q(Max)=(X(N)-X(N-1))/(X(N)-X(1))

 

6.3.4.2. Grubbs

Grubbs test requires that the data is approximately normally distributed and thus it is accurate for larger values of n. For one-tailed tests the test statistic G is calculated for minimum and maximum observations separately as follows:

     

     

For a two-tailed test greater of the G_Min and G_Max values is tested against the two-tailed table value for the given alpha. Table G is accurate for both one and two-tail tests.

Example

Tietjen and Moore (1972) test the following sequence of numbers 199.31, 199.53, 200.19, 200.82, 201.92, 201.95, 202.18, 245.57 for outliers.

Grubbs’ Outlier Test

Alpha = 0.05

One-tailed tests

	Grubbs’ G	Table G	Pass/Fail
C1 G(Min)	0.4494	2.0317	Pass
G(Max)	2.4688	2.0317	**Fail**

G = Maximum deviation from mean / Standard Deviation

 

	Outlier Value
C1	245.57

 

6.3.4.3. ESD (Generalised Extreme Studentised Deviate)

While Dixon’s and Grubbs’ tests can detect one outlier at a time, the Generalized Extreme Studentised Deviate (ESD) test can be used to test several outliers simultaneously. It is basically a Grubbs’ test run several times on the same sample, each time testing and omitting the most extreme observation and reducing the degrees of freedom by one. The user specifies the maximum number of extreme values to be tested.

The ESD test is two-tailed.

Example

In this example Rosner (1983) searches for 10 outliers in a series of 54 numbers. Open GOODFIT, select Statistics 1 → Goodness of Fit Tests → Outlier Tests and select VitE (C8) as [Variable]. On the Output Options Dialogue enter 10 into the Number of outliers to test (ESD) box, check only the ESD test and click [Finish] to obtain the following results:

ESD Outlier Test

Alpha = 0.05

Two-tailed test

Number of outliers to check (ESD) = 10

	ESD Ri	Table Ri	Pass/Fail
C1 (Max) 1	3.1189	3.1588	Pass
C1 (Max) 2	2.9430	3.1514	Pass
C1 (Max) 3	3.1794	3.1439	**Fail**
C1 (Max) 4	2.8102	3.1362	Pass
C1 (Min) 5	2.8156	3.1282	Pass
C1 (Max) 6	2.8482	3.1201	Pass
C1 (Max) 7	2.2793	3.1118	Pass
C1 (Max) 8	2.3104	3.1032	Pass
C1 (Min) 9	2.1016	3.0945	Pass
C1 (Max) 10	2.0672	3.0854	Pass

Ri = Generalised Extreme Studentised Deviate

 

	Outlier Value
C1	5.34