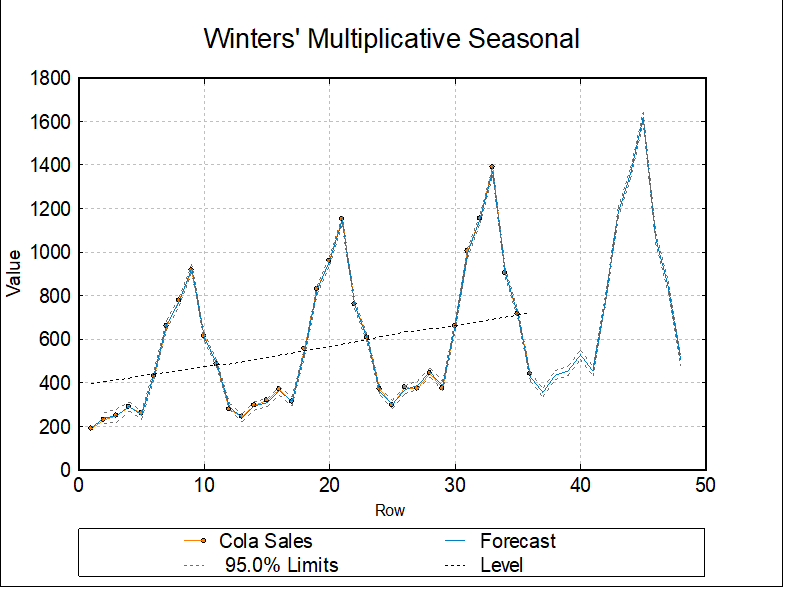
9.2.4. Winters’ Multiplicative Seasonal
This adds a mulitiplicative seasonal component to Holt’s Linear method. For a data series xt forecasts are given by:
where:
·
·
·
·
is the level smoothing constant,
·
is the trend smoothing constant,
·
is the seasonal smoothing constant,
· s is the season period.
The initial values are based on the complete data series. Suppose the series includes complete data for L seasons. The initial trend and level values are given by:
where:
·
is the average level in
season i.
The initial seasonal components c1-s, …, c0 are given by the average value of St, the observed value divided by the expected value if no seasonal component is used. That is:
where:
· i is the year in which t falls.
· j is season with in t falls.
Example
Consider the Tasty Cola Sales given in Table 6.4 Bowerman, Bruce L. & Richard T. O’Connell (1987). Open TIMESER and select Statistics 2 → Forecasting → Winters’ Multiplicative Seasonal and select Cola Sales (C2) as [Variable]. On the second dialogue enter:
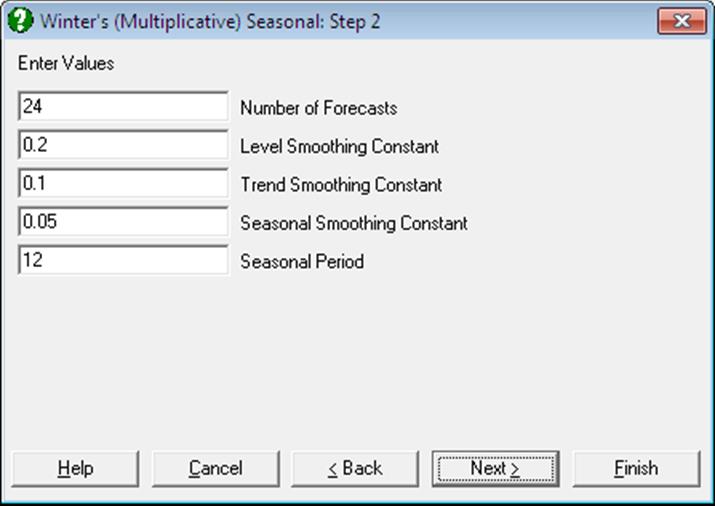
· 12 Number of Forecasts.
· .2 Level Smoothing Constant.
· .15 Trend Smoothing Constant.
· .05 Seasonal Smoothing Constant.
· 12 Seasonal Period.
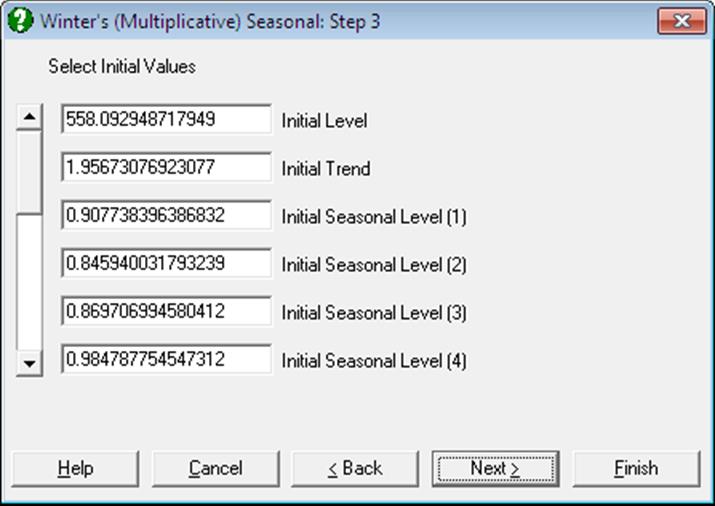
Select the default values on the third dialogue. Select the Summary Table on the Output Options Dialogue to obtain the following results. The table is shortened here for space considerations.
Winters’ Multiplicative Seasonal
|
Level Smoothing Constant = |
0.2000 |
|
Trend Smoothing Constant = |
0.1500 |
|
Seasonal Smoothing Constant = |
0.0500 |
|
Seasonal Period = |
12 |
|
Sum of Squares = |
2254.8254 |
Summary Table
|
Row |
Cola Sales |
Forecast |
Lower 95% |
Upper 95% |
Level |
Trend |
Seasonal |
|
1 |
189.0000 |
193.6418 |
* |
* |
398.0512 |
9.2853 |
0.4837 |
|
2 |
229.0000 |
238.1693 |
214.6797 |
261.6590 |
404.2000 |
8.8148 |
0.5838 |
|
3 |
249.0000 |
248.7039 |
217.7488 |
279.6590 |
413.1132 |
8.8296 |
0.6022 |
|
4 |
289.0000 |
291.9661 |
271.1169 |
312.8153 |
421.5858 |
8.9831 |
0.6909 |
|
5 |
260.0000 |
252.2613 |
233.9958 |
270.5268 |
433.2106 |
9.2472 |
0.5866 |
|
6 |
431.0000 |
440.9282 |
419.8437 |
462.0127 |
440.4653 |
9.0480 |
0.9956 |
|
7 |
660.0000 |
667.1568 |
645.5183 |
688.7952 |
448.5488 |
8.9515 |
1.4835 |
|
8 |
777.0000 |
774.4063 |
754.1714 |
794.6412 |
457.8068 |
8.9822 |
1.6929 |
|
9 |
915.0000 |
927.4468 |
909.2720 |
945.6216 |
465.5361 |
8.8569 |
1.9858 |
|
10 |
613.0000 |
611.8198 |
593.9592 |
629.6805 |
474.5760 |
8.8752 |
1.2898 |
|
11 |
485.0000 |
487.0187 |
470.7199 |
503.3175 |
483.0504 |
8.8351 |
1.0072 |
|
12 |
277.0000 |
292.4919 |
277.2284 |
307.7553 |
486.6750 |
8.3141 |
0.5934 |
|
13 |
244.0000 |
239.4143 |
220.1039 |
258.7248 |
496.8852 |
8.5037 |
0.4840 |
|
14 |
296.0000 |
295.0392 |
275.4274 |
314.6510 |
505.7181 |
8.5366 |
0.5839 |
|
15 |
319.0000 |
309.6720 |
291.1731 |
328.1710 |
517.3527 |
8.8464 |
0.6029 |
|
16 |
370.0000 |
363.5268 |
343.7310 |
383.3225 |
528.0731 |
9.0338 |
0.6913 |
|
17 |
313.0000 |
315.0635 |
295.0703 |
335.0568 |
536.4034 |
8.9634 |
0.5864 |
|
18 |
556.0000 |
542.9897 |
523.6656 |
562.3139 |
547.9802 |
9.2248 |
0.9966 |
|
19 |
831.0000 |
826.6347 |
806.6055 |
846.6638 |
557.7935 |
9.2836 |
1.4839 |
|
20 |
960.0000 |
960.0143 |
940.6599 |
979.3688 |
567.0755 |
9.2835 |
1.6929 |
|
21 |
1152.0000 |
1144.5310 |
1126.1433 |
1162.9188 |
577.1112 |
9.3587 |
1.9863 |
|
22 |
759.0000 |
756.4226 |
738.4717 |
774.3735 |
586.8695 |
9.3987 |
1.2900 |
|
23 |
607.0000 |
600.5685 |
583.2110 |
617.9260 |
597.5453 |
9.5264 |
1.0076 |
|
24 |
371.0000 |
360.2125 |
342.9294 |
377.4955 |
610.7077 |
9.8900 |
0.5941 |
|
25 |
298.0000 |
300.3973 |
281.9785 |
318.8161 |
619.6072 |
9.7909 |
0.4839 |
|
26 |
378.0000 |
367.4819 |
349.3146 |
385.6493 |
633.0010 |
10.1512 |
0.5845 |
|
27 |
373.0000 |
387.7550 |
368.5888 |
406.9211 |
638.2576 |
9.6617 |
0.6020 |
|
28 |
443.0000 |
447.9353 |
427.2584 |
468.6123 |
646.4916 |
9.5190 |
0.6910 |
|
29 |
374.0000 |
385.4918 |
364.6530 |
406.3307 |
653.3489 |
9.0469 |
0.5858 |
|
30 |
660.0000 |
660.1998 |
638.4242 |
681.9754 |
662.3557 |
9.0409 |
0.9967 |
|
31 |
1004.0000 |
996.3279 |
975.2618 |
1017.3940 |
672.4306 |
9.1960 |
1.4844 |
|
32 |
1153.0000 |
1154.0077 |
1133.2125 |
1174.8028 |
681.5076 |
9.1781 |
1.6930 |
|
33 |
1388.0000 |
1371.9822 |
1351.7913 |
1392.1730 |
692.2985 |
9.4201 |
1.9873 |
|
34 |
904.0000 |
905.2261 |
885.0484 |
925.4038 |
701.5284 |
9.3915 |
1.2899 |
|
35 |
715.0000 |
716.3717 |
696.7190 |
736.0244 |
710.6477 |
9.3507 |
1.0076 |
|
36 |
441.0000 |
427.7323 |
408.5459 |
446.9188 |
724.4651 |
10.0207 |
0.5948 |
|
37 |
|
355.4162 |
335.2428 |
375.5896 |
|
|
|
|
38 |
|
435.1913 |
414.5975 |
455.7850 |
|
|
|
|
39 |
|
454.2166 |
433.1702 |
475.2630 |
|
|
|
|
40 |
|
528.3472 |
506.8178 |
549.8765 |
|
|
|
|
41 |
|
453.7447 |
431.7040 |
475.7853 |
|
|
|
|
42 |
|
781.9787 |
759.4004 |
804.5570 |
|
|
|
|
43 |
|
1179.5346 |
1156.3941 |
1202.6751 |
|
|
|
|
44 |
|
1362.2084 |
1338.4830 |
1385.9339 |
|
|
|
|
45 |
|
1618.9822 |
1594.6506 |
1643.3139 |
|
|
|
|
46 |
|
1063.7802 |
1038.8227 |
1088.7376 |
|
|
|
|
47 |
|
841.0292 |
815.4278 |
866.6306 |
|
|
|
|
48 |
|
502.4411 |
476.1790 |
528.7033 |
|
|
|
